Main Menu
Write A Recursive Program To Solve Towers Of Hanoi Problem
понедельник 30 марта admin 22
This challenge helps you use your programming talents to write a Java program that will print the steps needed to solve a Towers of Hanoi puzzle given the number of disks.
The Towers of Hanoi is a classic logic puzzle that consists of three vertical pegs and a number of disks of various diameters. Each disk has a hole in the center, allowing the disks to be slipped over the pegs.
First, you can solve the Towers of Hanoi problem recursively. If n = 1 n = 1 n = 1 n, equals, 1, just move disk 1. Otherwise, when n ≥ 2 n geq 2 n ≥ 2 n, is greater than or equal to, 2, solve the problem in three steps.
The puzzle starts with all of the disks stacked on one of the pegs, with the largest disk at the bottom and the smallest at the top. The object of the puzzle is to move the stack of disks to one of the other pegs, obeying just two simple rules: (1) you can move only one disk at a time, and (2) you can never place a larger disk on top of a smaller one.
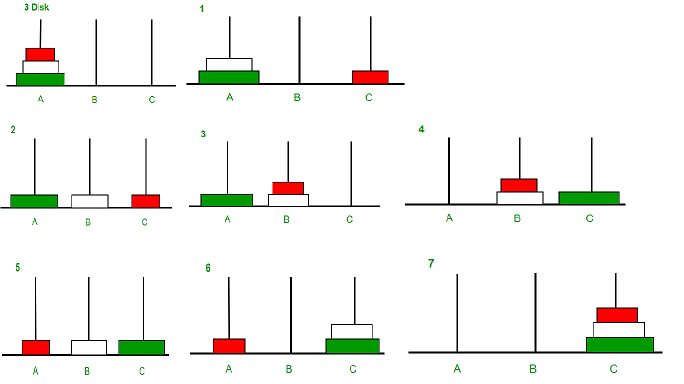
The following figure shows the solution for a stack of three disks. As you can see, the solution requires seven moves:
Move Disk 1 from Peg 1 to Peg 3. Delete power plan windows 10.
Move Disk 2 from Peg 1 to Peg 2.
Move Disk 1 from Peg 3 to Peg 2.
Move Disk 3 from Peg 1 to Peg 3.
Move Disk 1 from Peg 2 to Peg 1.
Move Disk 2 from Peg 2 to Peg 3.
Move Disk 1 from Peg 1 to Peg 3.
After these seven steps, the stack of disks will be on Peg 3.
The puzzle gets interesting when you begin adding disks to the starting position. With three disks, the puzzle requires just 7 moves to solve. With four disks, 15 moves are required. With five disks, you’ll need 31 moves. Six disks requires 64 moves.
If you’ve been following the math, the number of moves required to solve the puzzle increases exponentially as the number of disks increases. Specifically, the number of moves required to move n disks is 2n– 1. For example, a stack of 20 disks will require 220 – 1 moves; that’s more than a million moves!
An interesting legend is associated with the puzzle: At a temple in Hanoi, monks have been working on a Towers of Hanoi puzzle with 64 disks since the creation of the earth. When they finish, the world will come to an end. Fortunately, we have a long time to wait: If the monks can move one disk per second, it will be another 580 billion years or so before they finish the puzzle.
Your challenge is simple: Write a Java program that will print the steps needed to solve a Towers of Hanoi puzzle given the number of disks. The program should first prompt the user for the number of disks. Then it should display the steps, one per line. Each step should indicate which peg to move a disk from, and which peg to move the disk to. The steps should also be sequentially numbered.
Once finished, the program should repeat, asking the user for the number of disks again. The program should end when the user enters 0.
Here is a sample of the console output your program should generate:
The only other requirement for solving this challenge is that your solution must use recursive programming. In other words, your solution must include a method that calls itself to solve the puzzle.
Recursive programming can be challenging, so here are a few hints to the solution of this puzzle:
The puzzle consists of three pegs. One of them contains the starting stack of disks; call this peg the source peg. One of the remaining two pegs is the peg you want to move the stack of disks to; call this peg the target peg. The third peg is available for you to use as an intermediate peg to store disks on temporarily as you move them. Call this peg the spare peg.
Your recursive method should accept three parameters: the number of disks to move, source peg, and the target peg. Use the integer values 1, 2, and 3 to represent the pegs.
The basic idea of solving the puzzle recursively is this: To move a stack of disks from a source peg to a target peg requires three steps:
Move all of the disks in the stack except for the bottom disk to the spare peg.
Move the largest disk in the original stack to the target peg.
Move the stack you moved in Step 1 from the spare peg to the target peg.
Vol. 13 no. 51. P. 54, 56. What is pagemaker software. Borzo, Jeanette (December 7, 1992).
Of course, puzzle rules allow you to move only one disk at a time, so you can’t accomplish Steps 1 and 3 of the procedure given here by simply picking up the stack and moving it. That’s where the recursion comes in. For Steps 1 and 3, you call the method recursively, each time specifying one fewer disk to be moved, and each time using the previous target peg as the spare peg.
Wondering why the recursive method doesn’t need to accept the spare peg as an argument? Because you can easily calculate it, given the source and target pegs. Since there are only three pegs, numbered 1, 2, and 3, the sum of the three pegs is 6 (1+2+3). Given the source and target pegs, you can calculate the spare peg by subtracting the source and target peg from 6. For example, if the source peg is 1 and the target peg is 3, the spare peg must be 2 because
6 – 3 – 1 = 2.
For the solution, go to the Downloads tab of the Java All-in-One For Dummies, 4th Edition product page.
Good luck!
This challenge helps you use your programming talents to write a Java program that will print the steps needed to solve a Towers of Hanoi puzzle given the number of disks.
The Towers of Hanoi is a classic logic puzzle that consists of three vertical pegs and a number of disks of various diameters. Each disk has a hole in the center, allowing the disks to be slipped over the pegs.
The puzzle starts with all of the disks stacked on one of the pegs, with the largest disk at the bottom and the smallest at the top. The object of the puzzle is to move the stack of disks to one of the other pegs, obeying just two simple rules: (1) you can move only one disk at a time, and (2) you can never place a larger disk on top of a smaller one.
The following figure shows the solution for a stack of three disks. As you can see, the solution requires seven moves:
Move Disk 1 from Peg 1 to Peg 3.
Move Disk 2 from Peg 1 to Peg 2.
Move Disk 1 from Peg 3 to Peg 2.
Move Disk 3 from Peg 1 to Peg 3.
Move Disk 1 from Peg 2 to Peg 1.
Move Disk 2 from Peg 2 to Peg 3.
Move Disk 1 from Peg 1 to Peg 3.
After these seven steps, the stack of disks will be on Peg 3.
The puzzle gets interesting when you begin adding disks to the starting position. With three disks, the puzzle requires just 7 moves to solve. With four disks, 15 moves are required. With five disks, you’ll need 31 moves. Six disks requires 64 moves.
If you’ve been following the math, the number of moves required to solve the puzzle increases exponentially as the number of disks increases. Specifically, the number of moves required to move n disks is 2n– 1. For example, a stack of 20 disks will require 220 – 1 moves; that’s more than a million moves!
An interesting legend is associated with the puzzle: At a temple in Hanoi, monks have been working on a Towers of Hanoi puzzle with 64 disks since the creation of the earth. When they finish, the world will come to an end. Fortunately, we have a long time to wait: If the monks can move one disk per second, it will be another 580 billion years or so before they finish the puzzle.
Your challenge is simple: Write a Java program that will print the steps needed to solve a Towers of Hanoi puzzle given the number of disks. The program should first prompt the user for the number of disks. Then it should display the steps, one per line. Each step should indicate which peg to move a disk from, and which peg to move the disk to. The steps should also be sequentially numbered.
Once finished, the program should repeat, asking the user for the number of disks again. The program should end when the user enters 0.
Here is a sample of the console output your program should generate:
The only other requirement for solving this challenge is that your solution must use recursive programming. In other words, your solution must include a method that calls itself to solve the puzzle.
Recursive programming can be challenging, so here are a few hints to the solution of this puzzle:
The puzzle consists of three pegs. One of them contains the starting stack of disks; call this peg the source peg. One of the remaining two pegs is the peg you want to move the stack of disks to; call this peg the target peg. The third peg is available for you to use as an intermediate peg to store disks on temporarily as you move them. Call this peg the spare peg.
Your recursive method should accept three parameters: the number of disks to move, source peg, and the target peg. Use the integer values 1, 2, and 3 to represent the pegs.
The basic idea of solving the puzzle recursively is this: To move a stack of disks from a source peg to a target peg requires three steps:
Move all of the disks in the stack except for the bottom disk to the spare peg.
Move the largest disk in the original stack to the target peg.
Move the stack you moved in Step 1 from the spare peg to the target peg.
Of course, puzzle rules allow you to move only one disk at a time, so you can’t accomplish Steps 1 and 3 of the procedure given here by simply picking up the stack and moving it. That’s where the recursion comes in. For Steps 1 and 3, you call the method recursively, each time specifying one fewer disk to be moved, and each time using the previous target peg as the spare peg.
Wondering why the recursive method doesn’t need to accept the spare peg as an argument? Because you can easily calculate it, given the source and target pegs. Since there are only three pegs, numbered 1, 2, and 3, the sum of the three pegs is 6 (1+2+3). Given the source and target pegs, you can calculate the spare peg by subtracting the source and target peg from 6. For example, if the source peg is 1 and the target peg is 3, the spare peg must be 2 because
6 – 3 – 1 = 2.
For the solution, go to the Downloads tab of the Java All-in-One For Dummies, 4th Edition product page.
Good luck!